Combinatorial optimization involves optimization over discrete sets where a feasible solution is a combinatorial object such as a graph, permutation, set etc. Such problems are motivated by a diverse range of applications including logistics, manufacturing and telecommunications systems.
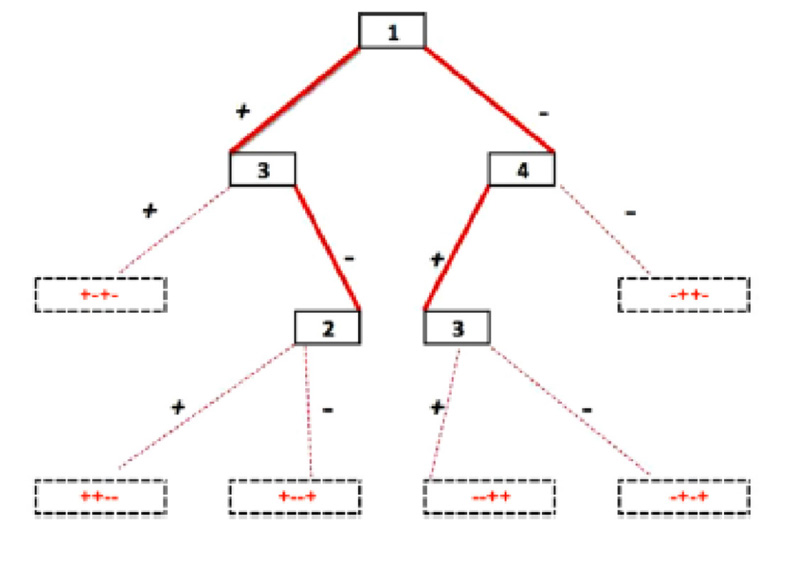
We consider various “optimal search” problems where the goal is to detect a hidden object by utilizing costly tests. The goal could be minimizing the expected cost or optimizing another performance metric regarding the accuracy of the conclusion. One can also consider other variations where the goal is classify an unknown Boolean vector correctly with the minimum cost.
We also study frequency assignment and routing problems in wireless telecommunication networks.